
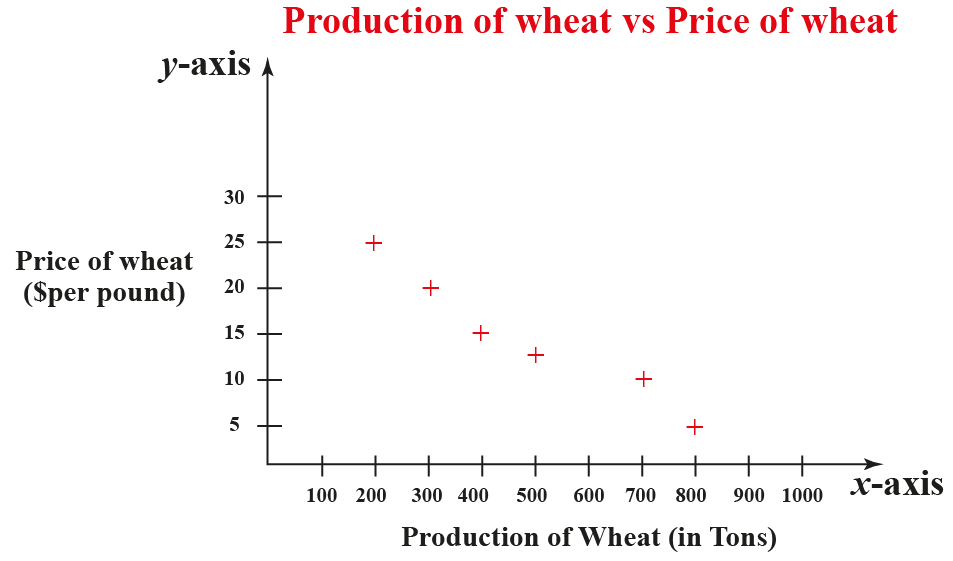
This scatter plot takes multiple scalar variables and uses them for different axes in phase space. In the scatterplot below, there is one outlier.A 3D scatter plot allows the visualization of multivariate data. Outliers are points that deviate from the pattern of the relationship. We develop a more precise way to measure the strength of a relationship shortly. This is an example of a weaker linear relationship.Labeling a relationship as strong or weak is not very precise. The data is more scattered about the line. In the bottom scatterplot, the data points also follow a linear pattern, but the points are not as close to the line. This is an example of a strong linear relationship. Let’s look, for example, at the following two scatterplots displaying positive, linear relationships: In the top scatterplot, the data points closely follow the linear pattern. The strength of the relationship is a description of how closely the data follow the form of the relationship.We study some specific types of curvilinear forms with their equations in Modules 4 and 12. We use a curve to summarize the pattern in the data. Curvilinear form: The data points appear scattered about a smooth curve. We study the equation for a line in this module. We use a line to summarize the pattern in the data. Here are a couple of forms that are quite common: Linear form: The data points appear scattered about a line. For now, we simply describe the shape of the pattern in the scatterplot.

We look at a few of these equations in this course. In practice, forms that we commonly use have mathematical equations. To identify the form, describe the shape of the data in the scatterplot. The form of the relationship is its general shape.Not all relationships can be classified as either positive or negative. The direction of the relationship can be positive, negative, or neither: A positive (or increasing) relationship means that an increase in one of the variables is associated with an increase in the other.Ī negative (or decreasing) relationship means that an increase in one of the variables is associated with a decrease in the other.Deviations from the pattern are still called outliers. Similarly, in a scatterplot, we describe the overall pattern with descriptions of direction, form, and strength. We also describe deviations from the pattern (outliers). To describe the overall pattern of the distribution of one quantitative variable, we describe the shape, center, and spread. This is the same way we described the distribution of one quantitative variable using a dotplot or a histogram in Summarizing Data Graphically and Numerically. How do we describe the relationship between two quantitative variables using a scatterplot? We describe the overall pattern and deviations from that pattern. Describe the overall pattern (form, direction, and strength) and striking deviations from the pattern. Use a scatterplot to display the relationship between two quantitative variables.


 0 kommentar(er)
0 kommentar(er)
